정리) 렐루 함수는 로지스틱 함수와 하이퍼볼릭 탄젠트가 z가 커졌을 때, 그레디언트가 작아져 훈련이 느려지는 문제를 해결한다.
렐루(Rectified Linear Unit, ReLU)
렐루는 심층 신경망에 자주 사용되는 활성화 함수 중 하나이다.
그레디언트 소실 문제(vanishing gradient problem)
하이퍼볼릭 탄젠트와 로지스틱 회귀 함수는 최종 입력에 대한 활성화 함수의 도함수가 z가 커짐에 따라서 줄어든다.
그레디언트가 0에 아주 가까워 지기 때문에 훈련 과정 동안 가중치가 매우 느리게 학습된다.
렐루 함수는 이러한 문제를 해결할 수 있다.
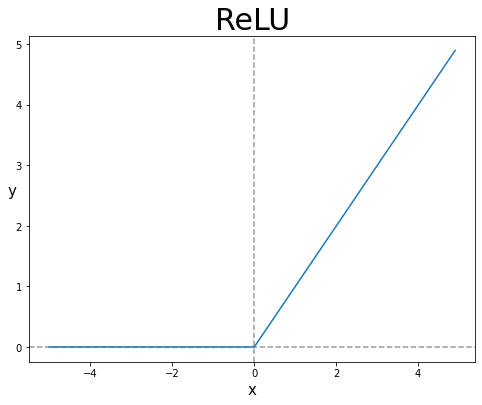
렐루 함수도 신경망이 복잡한 함수를 학습하기에 좋은 비선형 함수이다.
입력 값이 양수이면 입력에 대한 렐루의 도함수는 항상 1이다.(그레이디언트 소실 문제 해결)
tf.keras.activations.relu(z)
<tf.Tensor: shape=(2000,), dtype=float64, numpy=array([0. , 0. , 0. , ..., 4.985, 4.99 , 4.995])>
linear한 연산을 갖는 layer를 수십개 쌓아도 결국 이는 하나의 linear 연산으로 나타낼 수 있다.
이에 대한 해결책이 바로 활성화 함수(activation function)이다.
활성화 함수를 사용하면 입력값에 대한 출력값이 linear하게 나오지 않으므로 선형분류기를 비선형 시스템으로 만들 수 있다.
* 따라서 MLP(Multiple layer perceptron)는 단지 linear layer를 여러개 쌓는 개념이 아닌 활성화 함수를 이용한 non-linear 시스템을 여러 layer로 쌓는 개념이다